Tiếp tục bài viết, mình sẽ cho các bạn giải thích cho các bạn về các tính chất của hàm Softmax và chứng minh một thành phần rất quan trọng để đánh giá mô hình trong quá trình học là Loss function.

3. Ý nghĩa và tính chất của hàm Softmax Function and hàm Loss Cross-Entropy:

Trong phần này mình sẽ hướng dẫn các bạn chứng minh toán học công thức của Softmax Regression và hàm mất mát Cross-Entropy.

3.1. Softmax function

Ở đây mình sẽ không chứng minh hàm Sigmoid hay hàm Softmax. Chúng ta sẽ chỉ xem xét các tính chất đặc trưng của các hàm này. Trước khi nói về hàm Softmax thì mình sẽ nói về hàm Sigmoid trước. Hàm Sigmoid có những tính chất quan trọng sau (hình 11, hình 12):

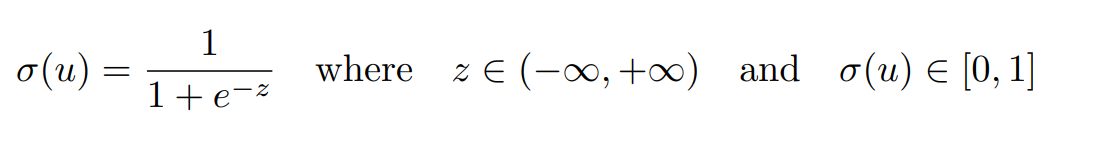Hình 11 – Tính chất 1

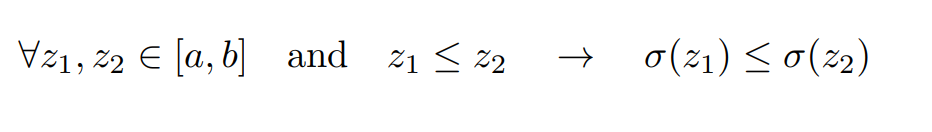Hình 12 – Tính chất 2

Đối với tính chất 1, mọi giá trị z đi qua hàm sigmoid thuộc khoảng từ âm vô cùng đến dương vô cùng, và khi đi qua hàm sigmoid chúng nằm trong khoảng từ 0 đến 1. Chúng ta có thể hiểu nôm na đó là giá trị xác suất. Còn đối với tính chất 2, đây là một tính chất vô cùng quan trọng trong bài toán phân loại. Khi mỗi node đưa ra một giá trị xác suất, trong ngữ cảnh của học máy, chúng ta thường không quan tâm đến giá trị của nó bao nhiêu, mà chúng ta thường sẽ quan tâm về đâu là giá trị lớn hơn, giá trị nào nhỏ hơn, giá trị nào lớn nhất và giá trị nào nhỏ nhất.

Mình có một ví dụ sau đây: giả sử mô hình của chúng ta thực hiện một nhiệm vụ phân loại 2 loài hoa với đầu ra lần lượt là y1 = 0.4, y2 = 0.6. Khi chúng ta phân loại chúng ta sẽ chỉ quan tâm đến lớp có xác suất cao nhất là y2 trong các đầu ra và các xác suất còn lại trong ngữ cảnh này không còn quan trọng. Và tính chất 2 này cũng tương tự với hàm Softmax, ngoại trừ việc nó có thể đưa ra xác suất của nhiều hơn 2 lớp.

3.1. Hàm loss function 

Phần này mình sẽ giải thích về cách Loss function thật sự có nghĩa là gì qua hình 13, hình 14:

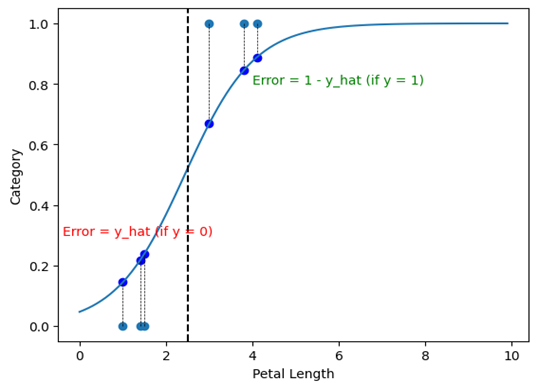Hình 13 – Minh hoạ về Error

Hình 14 - Chứng minh Binary-Cross Entropy

Như vậy mình đã chứng minh hàm Binary-Cross Entropy ở góc nhìn xác suất được sử dụng trong mô hình Logistic Regression. 

Tổng quát hoá lên chúng ta có được hàm Cross-Entropy cho mô hình Softmax Regression có khả năng tính được sự mất mát cho bài toán Multi-class classification:

Hình 15 - Pipeline về Softmax Regression

Ở đây chắc nhiều bạn lại tự hỏi rằng vì sao chúng ta lại sử dụng hàm Cross-Entropy mà không phải các hàm toán khác như mean-square error, dưới đây mình sẽ cho các bạn thấy được sự ảo diệu của hàm Cross-entropy. Giả sử ta có một tập dữ liệu như bên dưới, và chúng ta quan tâm đến sample có Petal Length là 1.3 và có Label là 0 (hình 16):

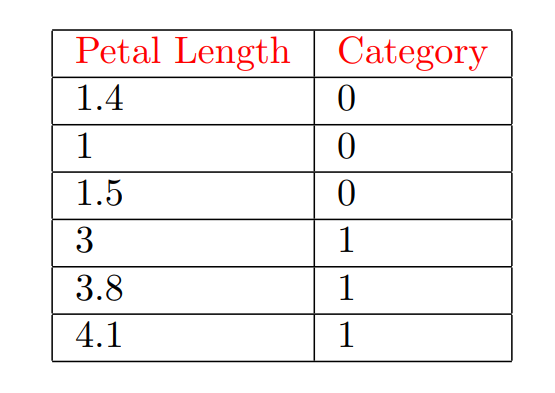Hình 16 - Minh hoạ Iris 1D dataset

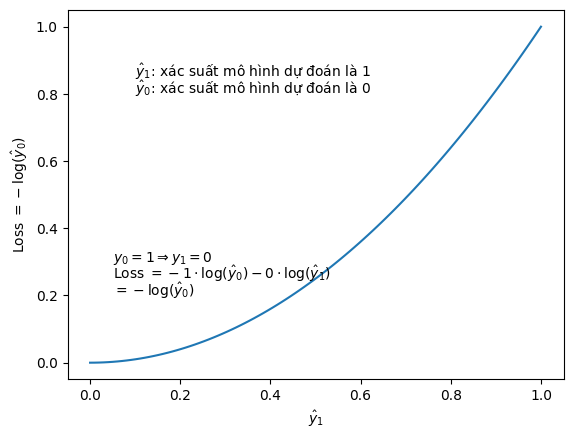Hình 17 - Binary Cross-Entropy trong trường hợp nhãn là 0

Từ hình trên ta nhận xét rằng: khi giá trị dự đoán đối với trường hợp label = 0, thì khi y_hat (y mũ) càng gần 1 thì loss càng nhỏ, còn khi y_hat càng xa giá trị 1 thì Loss càng lớn. Điều này là cần thiết cho một hàm Loss function bởi vì khi giá trị dự đoán càng xa so với thực tế, ta cần một hàm có thể tính được độ mất mát này, chúng ta có thể hiểu nôm na là khi độ mất mát so với giá trị thực tế càng cao, mô hình sẽ càng phạt nặng để mô hình có thể tiến đến thực tế càng nhanh. Còn khi giá trị dự đoán càng gần với thực tế thì loss phải thực sự nhỏ để mô hình biết là nó đã dự đoán rất gần với thực tế.

4. Tổng kết

Như vậy qua bài này, mình đã trình bày cho các bạn về thuật toán Softmax Regression từ ý tưởng của 2 thuật toán Linear Regression và Logistic Regression. Ngoài ra phần cuối mình đã trình bày cho các bạn thấy về một số ý nghĩa của các công thức toán học phổ biến như hàm mất mát Cross-Entropy hay hàm Softmax Regression. Bài viết này mình cũng muốn cho các bạn những cảm quan đầu tiên về Neural Network, các bài sau chúng ta sẽ cùng thảo luận kỹ hơn về Deep Learning và các thành phần bên trong nó.

print("Hello World")
System.out.println("Hello World")

Bài viết đượcc thực hiện bởi: